双指针模板

双指针技巧可以分为两类

「快慢指针」 解决主要解决链表中的问题，比如典型的判定链表中是否包含环
「左右指针」 后者主要解决数组（或者字符串）中的问题，比如二分查找、滑动窗口

一、快慢指针的常见算法

快慢指针一般都初始化指向链表的头结点 head，前进时快指针 fast 在前，慢指针 slow 在后，巧妙解决一些链表中的问题。

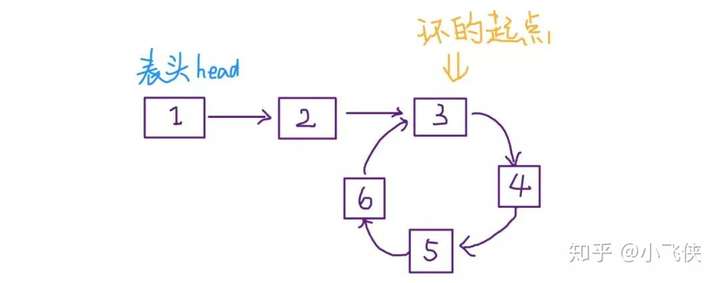
1、判定链表中是否含有环

这应该属于链表最基本的操作了，如果读者已经知道这个技巧，可以跳过。

单链表的特点是每个节点只知道下一个节点，所以一个指针的话无法判断链表中是否含有环的。

如果链表中不包含环，那么这个指针最终会遇到空指针 null 表示链表到头了，这还好说，可以判断该链表不含环。

boolean hasCycle(ListNode head) {
    while (head != null)
        head = head.next;
    return false;
}

但是如果链表中含有环，那么这个指针就会陷入死循环，因为环形数组中没有 null 指针作为尾部节点。

经典解法就是用两个指针，一个每次前进两步，一个每次前进一步。如果不含有环，跑得快的那个指针最终会遇到 null，说明链表不含环；如果含有环，快指针最终会超慢指针一圈，和慢指针相遇，说明链表含有环。

boolean hasCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while(fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        
        if (fast == slow)
            return true;
    }
    return false;
}

2、已知链表中含有环，返回这个环的起始位置

这个问题其实不困难，有点类似脑筋急转弯，先直接看代码：

ListNode detectCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow)
            break;
    }
    
    slow = head;
    while (slow != fast) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

可以看到，当快慢指针相遇时，让其中任一个指针重新指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。这是为什么呢？

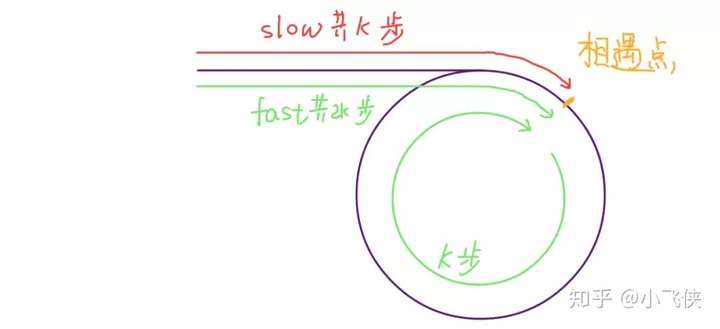
第一次相遇时，假设慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步，也就是说比 slow 多走了 k 步（也就是环的长度）。

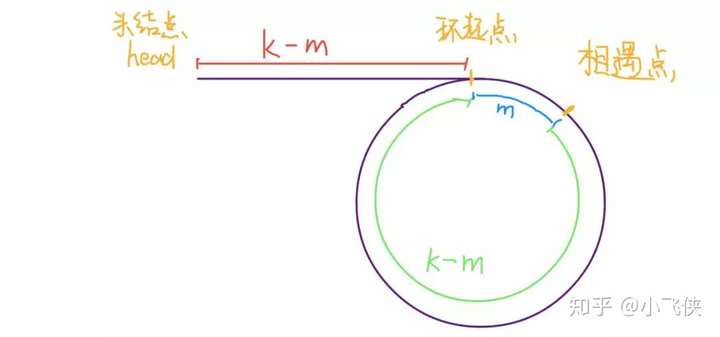
设相遇点距环的起点的距离为 m，那么环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。

巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。

所以，只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后就会相遇，相遇之处就是环的起点了。

3、寻找链表的中点

类似上面的思路，我们还可以让快指针一次前进两步，慢指针一次前进一步，当快指针到达链表尽头时，慢指针就处于链表的中间位置。

ListNode slow, fast;
slow = fast = head;
while (fast != null && fast.next != null) {
    fast = fast.next.next;
    slow = slow.next;
}
// slow 就在中间位置
return slow;

当链表的长度是奇数时，slow 恰巧停在中点位置；如果长度是偶数，slow 最终的位置是中间偏右：

寻找链表中点的一个重要作用是对链表进行归并排序。

回想数组的归并排序：求中点索引递归地把数组二分，最后合并两个有序数组。对于链表，合并两个有序链表是很简单的，难点就在于二分。

但是现在你学会了找到链表的中点，就能实现链表的二分了。关于归并排序的具体内容本文就不具体展开了。

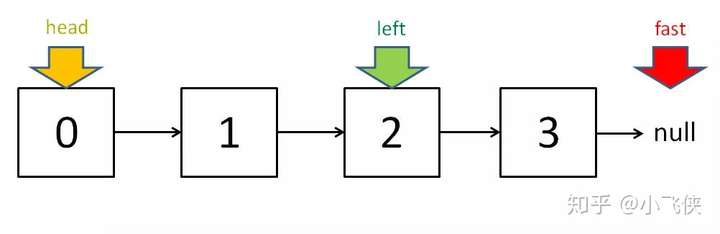
4、寻找链表的倒数第 k 个元素

我们的思路还是使用快慢指针，让快指针先走 k 步，然后快慢指针开始同速前进。这样当快指针走到链表末尾 null 时，慢指针所在的位置就是倒数第 k 个链表节点（为了简化，假设 k 不会超过链表长度）：

ListNode slow, fast;
slow = fast = head;
while (k-- > 0) 
    fast = fast.next;

while (fast != null) {
    slow = slow.next;
    fast = fast.next;
}
return slow;

二、左右指针的常用算法

左右指针在数组中实际是指两个索引值，一般初始化为 left = 0, right = nums.length - 1 。

1、二分查找

前文二分查找算法详解有详细讲解，这里只写最简单的二分算法，旨在突出它的双指针特性：

int binarySearch(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    while(left <= right) {
        int mid = (right + left) / 2;
        if (nums[mid] == target)
            return mid;
        else if (nums[mid] < target)
            left = mid + 1;
        else if (nums[mid] > target)
            right = mid - 1;
    }
}

2、两数之和

直接看一道 LeetCode 题目吧：

只要数组有序，就应该想到双指针技巧。这道题的解法有点类似二分查找，通过调节 left 和 right 可以调整 sum 的大小：

3、反转数组

void reverse(int[] nums) {
    int left = 0;
    int right = nums.length - 1;
    while (left < right) {
        // swap(nums[left], nums[right])
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
        left++;
        right--;
    }
}

4、滑动窗口算法

如果掌握了此算法，可以解决一大类子字符串匹配的问题，详情参考滑动窗口一文。

参考：

https://zhuanlan.zhihu.com/p/138273078