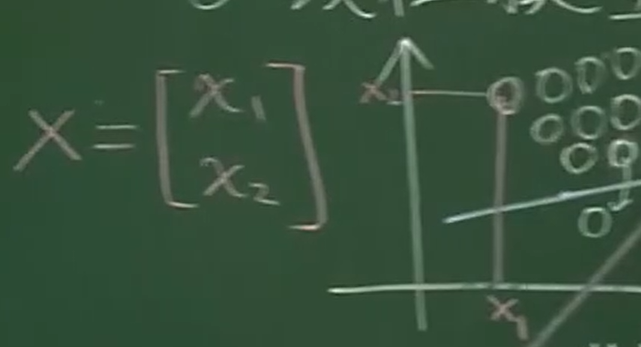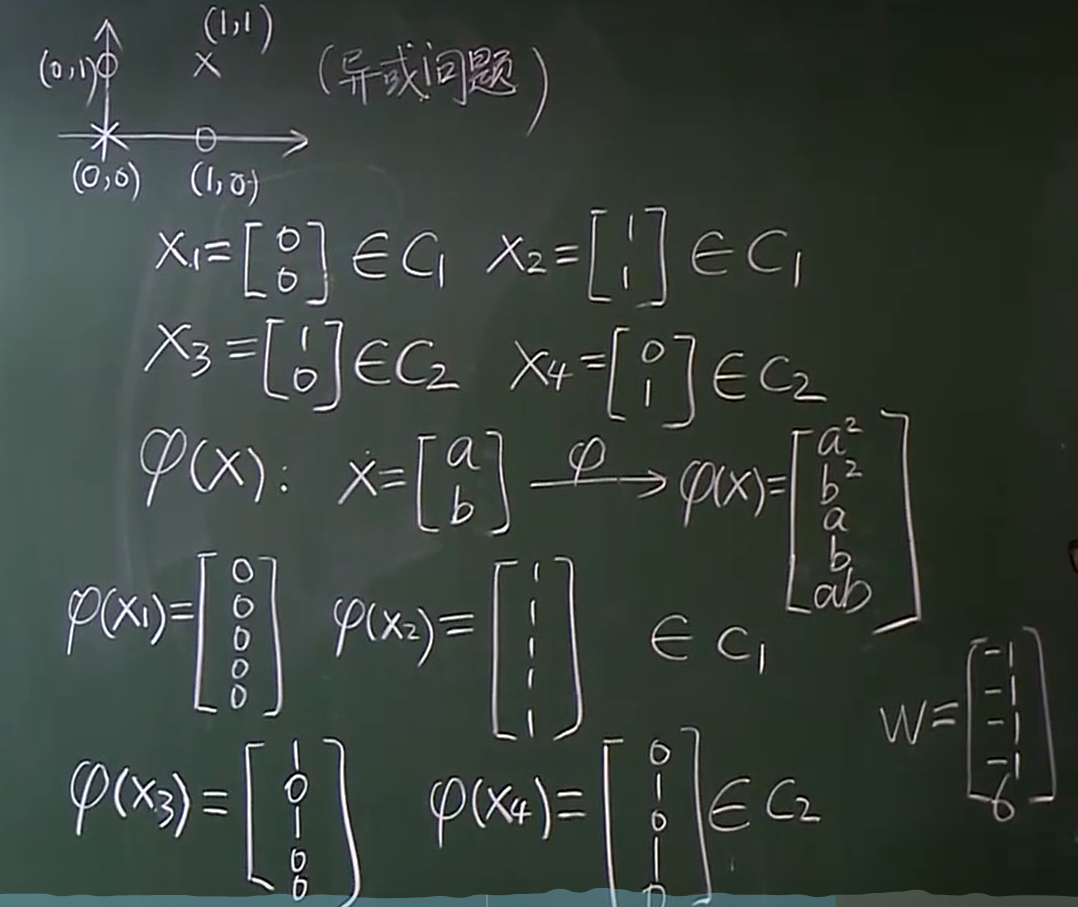SVM支持向量机

SVM （Support Vector Machine）。通常在样本数很少的情况下，使用支持向量机得到的结果都是很不错的。

设计思路

我们选想办法在线性可分样本集上找一条直线划分样本集，再想办法推广到非线性可分样本集上。

硬间隔支持向量机

如何在线性可分样本集上划分样本集？

首先，如果是存在一条直线可以划分样本集，那么在空间中就存在无数条直线可以划分。

那么哪一条直线是最好的？（划分标准）

首先我们希望划分线，对误差数据有更强的容忍度，如图中，2号线所示：

那么我们如果定义这条线呢？

  • 定义一个性能指标
  • 在这个性能指标下，2号线的性能最好

首先我们定义一条线，做其两条平行线，使两条平行线各自刚好接触到样本点，且这条线更好处于两条平行线中间。我们的性能指标就是希望这两条平行线的距离尽可能的大。

​ 其中我们定义：

​ 间隔：两条平行线直接的距离

​ 支持向量：将平行线插到的向量叫做支持向量 support vector

如何推导到这条线？（数学描述）

定义

  1. 训练数据和标签：（x1,y1），（x2,y2），（x3,y3）…（xn,yn）

    其中 X 是特征向量，如：image-20210812161920634

    其 Y 是标签，如：（-1和+1）

  2. 线性模型：（W,b）

    我们就是要在这个模型的限定下，求出W向量和常数b！

    总结：

    1. 先限定一个模型，如：此处的

    1. 留出待定的参数 ，如：此处的W和b

    2. 用样本数据带入模型，确定W和b

  3. 用数学定义训练集线性可分

    其中a,b等价于公式1

优化问题（凸优化问题，二次规划问题）

补充说明：二次规划问题

  1. 目标函数二次项是二次项
  2. 限制条件是一次性

其结果是，要么无解，要么只有一个极值。

所以，如何从上面的数学模型推导到一个二次规划问题，就是如下的工作。

线性模型的优化结论

最小化：

限制条件：

首先我们需要知道以下两个事实：

事实1：

​ 若（W,b）满足公式1，则（aW，ab）也满足公式1

事实2：点到平面的距离公式

​ 由此可以推导出，X特征向量到超平面的距离公式应为：

​

推导过程

有以上两个事实后，我们可以用a去缩放(W,b) —>(aW,ab) ,最终使支持向量X0上有：

此时支持向量与超平面的距离为：

即最小化||W||，就等于最大化支持向量与平面的距离。

而非支持向量到直线的距离就会大于d，即等于限制条件

其中此处的距离1，可以不取1而取其他值，最后得到的结果只是常数偏移，是同一个平面。

如此就将整个求解最大化支持向量间距的问题，用二次规划优化的形式描述了出来。

要求最大化支持向量间距，其目标函数就是要求最小化：

其限制条件为：

软间隔支持向量机

如何在部分点不可分，总体近似可分样本集上划分样本集？

软间隔支持向量机就是在硬间隔的基础上修改优化目标函数和限制条件

二次规划问题的优化函数

最小化：

​ 其中后面的叫正则项（让原来没有解的方式变得有解或变得更优解）

​ C是事先设定的参数，需要我们不断去试。

限制条件：

松弛变量是个新引入的值，他使得我们之前线性可分时所求解的硬间隔问题，变成了软间隔问题。即不再是要求每一个点都可分，而是求解一条直线近似满足到支持向量的距离最远。但是有了松弛变量后，为了规范其推演，防止其趋于无穷大，我们设置其大于0且尽可能的小。

核函数支持向量机

如何在线性不可分样本集上划分样本集？

虽然有了上述的软间隔支持向量机优化函数，我们已经可以通过SVM处理非线性问题，但他依然是在求解一条直线近似满足条件，而不是求解一条曲线。

我们已经可以在线性可分的样本中将样本分开，我们如何将其应用到非线性样本中？

提高维度

如这样一个异或问题，将其二分类。

image-20210812190218668

我们通过一个线性变化f(x) ，将二维的特征映射到更高的维度。这样使得在二维不线性可分的情况，在高维有线性可分的可能，且维度越高，可能性越大。

如此我们只需将原来的优化函数做一点维度上的改变：

同时引出了另外一个问题，f(x) 是无限维，那么该优化式如何求解？

核函数

我们可以不知道无限维映射f(x)的显式表达，我们只要知道一个核函数（Kernel function）

则上述的优化式依然可解。

其中核函数能写成上述形式，必须满足以下两个条件：

常用核函数

高斯核函数
多项式核函数

如上中的一个核函数，我们可以直接求出 X 的内积，避免在高维空间中求 $Φ(x_i)^TΦ(x_j)$

常用核函数

如何用推导出核函数？

补充《优化理论》知识

原问题(Prime problem) 具有普适性

​ 最小化：

​ 限制条件:

拉格朗日对偶定义：
对偶问题定义：

最大化：

​ 对所有的W求L()的最小值，对所有的alpha和beta求theta()的最大值

限制条件：

核函数就是将原问题转换为对偶问题求解。

后续推导过程暂略…..数学功底不够了……

SVM处理多分类问题

SVM更适合于二分类的问题，对于多分类有如下几种思路：

  • 改造优化的目标函数和限制条件，使之可以处理多分类问题。(不建议)

  • 一类 VS 其他类

    1
    2
    3
    4
    5
    c1 vs (c2c3) +1
    c2 vs (c1c3) -1
    c3 vs (c2c1) -1
    根据三个标签能判断出X属于哪一类，但如果无法判断，|W(X) + b| >=0,就看谁的距离阈值的值更大，即可能性更大。
    需要构造N个对比分类！

  • 一类 VS 另一类

    1
    2
    3
    4
    5
    c1 vs c2 +1
    c1 vs c3 +1
    c2 vs c3 -1
    根据票数来算，谁的票多，如：c1有两票，就预测为c1
    需要构造N(N-1)/2个对比分类！

    如果使用如决策树之类的，树状分类，会更适合多类别分类。

SVM的应用

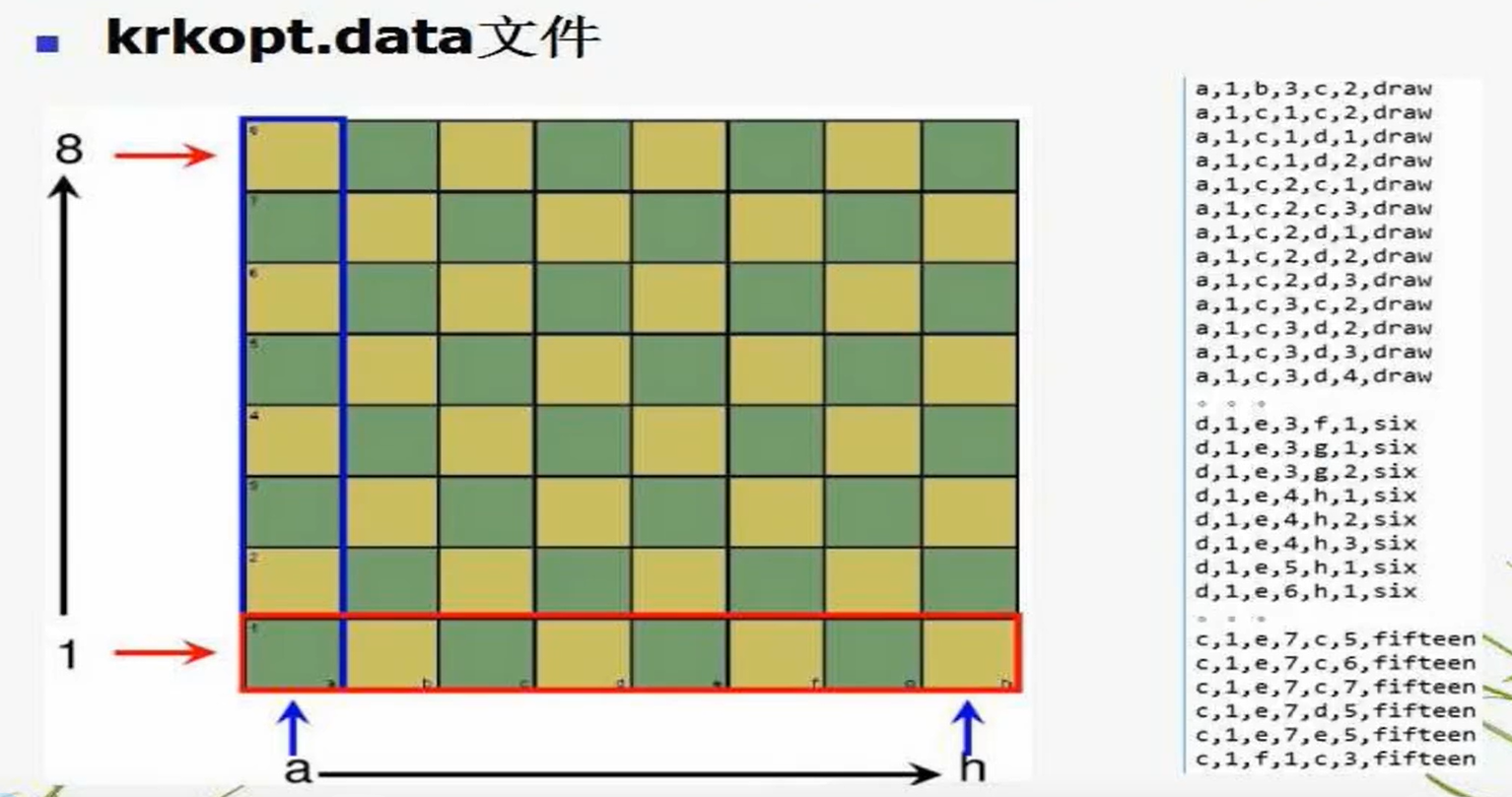
使用SVM解决兵王问题（白方一兵一王，黑方一王，在不同的位置下，结局不同）

  • 总样本数28056，正样本有2796，负样本有25260.

  • 随机取5000个做训练，其他做测试

  • 样本归一化，在训练样本上，求出每一个维度的均值和方差，在训练和测试样本上同时归一化

  • 选择高斯核模型

数据如下：

image-20210813133213875

其中，a-h表示横坐标，draw表示平局，six表示白方6步能取得胜利。

数据预处理

将横坐标和标签处理为数字

1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
import pandas as pd

data = pd.read_csv('krkopt.data',header=None)
def map1(x):
    return ord(x) - ord('a')
data[0] = data[0].map(map1)
data[2] = data[2].map(map1)
data[4] = data[4].map(map1)
def map2(x):
    if (x == 'draw'): return 0
    else: return 1
data[6] = data[6].map(map2)

数据标准化

1
2
3
4
from sklearn.preprocessing import StandardScaler 
# 标准化
transfer = StandardScaler()
data = transfer.fit_transform(data)

切分训练集和测试集

1
2
3
4
5
6
from sklearn.model_selection import train_test_split
# 切分训练集和测试集
x = data.loc[:,0:5]
y = data.loc[:,6:6]
y = y.values.ravel()
train_data,test_data,train_label,test_label=train_test_split(x,y,random_state=1,train_size=0.6,test_size=0.4)

交叉验证

1
2
3
4
5
model=svm.SVC(C=2,kernel='rbf',gamma=10,decision_function_shape='ovo') 
# 5 折 交叉验证
train_score = cross_val_score(model, train_data, train_label, cv=5)
print("训练集：",train_score)
print("Accuracy: %0.2f (+/- %0.2f)" % (train_score.mean(), train_score.std() * 2))

网格搜索参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 网格搜索参数 C,gamma
from sklearn.model_selection import GridSearchCV
param_grid = [
{'C': [2**i for i in range(-5,15)], 'gamma': [2**i for i in range(-5,3)]},
]

model=svm.SVC(kernel='rbf',decision_function_shape='ovo') 
gs = GridSearchCV(model, param_grid, refit = True, cv = 5, verbose = 1, n_jobs = -1)
gs.fit(train_data,train_label)

print('最优参数: ',gs.best_params_)
print('最佳性能: ', gs.best_score_)

test_score = gs.score(test_data,test_label)
print("测试集：",test_score)

Sklearn中SVM的简介

sklearn提供了三种基于svm的分类方法：

  • sklearn.svm.NuSVC()
  • sklearn.svm.LinearSVC()
  • sklearn.svm.SVC()

1. sklearn.svm.SVC()

全称是C-Support Vector Classification，是一种基于libsvm的支持向量机，由于其时间复杂度为O(n^2)，所以当样本数量超过两万时难以实现。

  • 官方源码：
1
2
3
4
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, 
                probability=False, tol=0.001, cache_size=200, class_weight=None, 
                verbose=False, max_iter=-1, decision_function_shape='ovr', 
                random_state=None)
  • 相关参数：
  1. C （float参数 默认值为1.0）
    表示错误项的惩罚系数C越大，即对分错样本的惩罚程度越大，因此在训练样本中准确率越高，但是泛化能力降低；相反，减小C的话，容许训练样本中有一些误分类错误样本，泛化能力强。对于训练样本带有噪声的情况，一般采用后者，把训练样本集中错误分类的样本作为噪声。
  2. kernel （str参数 默认为‘rbf’）
    该参数用于选择模型所使用的核函数，算法中常用的核函数有：
    — linear：线性核函数
    — poly：多项式核函数
    —rbf：径像核函数/高斯核
    —sigmod：sigmod核函数
    —precomputed：核矩阵，该矩阵表示自己事先计算好的，输入后算法内部将使用你提供的矩阵进行计算
  3. degree （int型参数 默认为3）
    该参数只对’kernel=poly’(多项式核函数)有用，是指多项式核函数的阶数n，如果给的核函数参数是其他核函数，则会自动忽略该参数。
  4. gamma （float参数 默认为auto）
    该参数为核函数系数，只对‘rbf’,‘poly’,‘sigmod’有效。如果gamma设置为auto，代表其值为样本特征数的倒数，即1/n_features，也有其他值可设定。
  5. coef0:（float参数 默认为0.0）
    该参数表示核函数中的独立项，只有对‘poly’和‘sigmod’核函数有用，是指其中的参数c。
  6. probability（ bool参数 默认为False）
    该参数表示是否启用概率估计。 这必须在调用fit()之前启用，并且会使fit()方法速度变慢。
  7. shrinkintol: float参数 默认为1e^-3g（bool参数 默认为True）
    该参数表示是否选用启发式收缩方式。
  8. tol（ float参数 默认为1e^-3）
    svm停止训练的误差精度，也即阈值。
  9. cache_size（float参数 默认为200）
    该参数表示指定训练所需要的内存，以MB为单位，默认为200MB。
  10. class_weight（字典类型或者‘balance’字符串。默认为None）
    该参数表示给每个类别分别设置不同的惩罚参数C，如果没有给，则会给所有类别都给C=1，即前面参数指出的参数C。如果给定参数‘balance’，则使用y的值自动调整与输入数据中的类频率成反比的权重。
  11. verbose （ bool参数 默认为False）
    该参数表示是否启用详细输出。此设置利用libsvm中的每个进程运行时设置，如果启用，可能无法在多线程上下文中正常工作。一般情况都设为False，不用管它。
  12. max_iter （int参数 默认为-1）
    该参数表示最大迭代次数，如果设置为-1则表示不受限制。
  13. random_state（int，RandomState instance ，None 默认为None）
    该参数表示在混洗数据时所使用的伪随机数发生器的种子，如果选int，则为随机数生成器种子；如果选RandomState instance，则为随机数生成器；如果选None,则随机数生成器使用的是np.random。
  • 方法
  1. svc.decision_function(X)
    样本X到分离超平面的距离
  2. svc.fit(X, y[, sample_weight])
    根据给定的训练数据拟合SVM模型。
  3. svc.get_params([deep])
    获取此估算器的参数并以字典行书储存,默认deep=True，以分类iris数据集为例，得到的参数如下
1
2
3
4
{'C': 1.0, 'cache_size': 200, 'class_weight': None, 'coef0': 0.0,
'decision_function_shape': 'ovr', 'degree': 3, 'gamma': 'auto', 'kernel': 'rbf', 
'max_iter': -1, 'probability': False, 'random_state': None, 'shrinking': True, 
'tol': 0.001, 'verbose': False}
  1. svc.predict(X)
    根据测试数据集进行预测
  2. svc.score(X, y[, sample_weight])
    返回给定测试数据和标签的平均精确度
  3. svc.predict_log_proba(X_test)，svc.predict_proba(X_test)
    当sklearn.svm.SVC(probability=True)时，才会有这两个值，分别得到样本的对数概率以及普通概率。

参考：

https://www.bilibili.com/video/BV1dJ411B7gh?p=11

https://murphypei.github.io/blog/2019/02/svm-kernel

https://segmentfault.com/a/1190000022278707

https://www.jianshu.com/p/a9f9954355b3